Ю.М. Печатников, А. Е. Шпарбер
СанктПетербургский государственный политехнический университет
195297, Санкт-Петербург, Политехническая ул., д.29,
E-mail: yiriy@nm.ru
В настоящее время учет совокупности всех взаимосвязанных и, зачастую, противоречивых факторов базируется на интуитивно-эмпирическом опыте конструктора, для которого характерны рассуждения, описание ситуаций и объектов на естественном для него языке в условиях неопределенности или отсутствия многих количественных зависимостей между показателями качества и проектными характеристиками [1,2].
На современном уровне в связи с активным развитием аппаратных средств, средств коммуникации и программного обеспечения возникает возможность кардинально обновить и улучшить подход к проектированию на базе современных достижений интеллектуально-информационной технологии: методов нечеткой логики, теории принятия решений, специальных моделей, знаний, опыта, данных. Сложность данной проблемы обусловлена не только наличием противоречивых требований, лежащих в основе тех или иных процедур, но и объективными ограничениями, налагаемыми заказчиком и спецификой производства [3].
В связи с этим одной из задач видится в создании автоматизированных систем поддержки инженерных решений на всех этапах и процедурах, в том числе и на этапе технического предложения.
Автоматизированная система поддержки функциональных инженерных решений (САПФИР) может быть полезной при решении широкого круга задач расчета и оптимизации конкретной вакуумной системы, прогнозирования конкурентоспособности проектируемого оборудования [2,3].
Процесс проектирования сoстоит из структурного синтеза, параметрического синтеза, анализа ведется на основе данных, экспертных оценок и знаний, которые структурированы и формализованы в базы данных и знаний [4,5]. База данных содержит информацию о технико-экономических характеристиках современных вакуумных систем и их элементов, а также включает типовые вакуумные схемы. База знаний содержит теоретические и эвристические методы и правила, экспертные оценки, факты (данные) и правила, использующие их, как основу для принятия решений. Общая задача проектирования разбивается на отдельные процедуры, описываемые моделями разной сложности и для решения каждой из которых используется свои наиболее адекватные предназначенные для них методы и средства. Отметим, что в процессе проектирования успешно сочетаются математически строгие методы с экспертными оценками и эмпирическими правилами.
САПФИР может быть использована при фундаментальных исследованиях широкого круга проблем, связанных с выявлением ранее неизвестных фактов и закономерностей техники получения вакуума, объяснения явлений имеющих место при течении разреженного газа.
В данном докладе представляется более подробно процедура и алгоритм проведения вычислительных экспериментов при молекулярно-вязкостном режиме.
Исследование в молекулярном и молекулярно-вязкостном режиме при вычислительных экспериментах ведутся методами прямого моделирования (метод Г. Берда) и статистических испытаний [2].
В настоящее время метод прямого моделирования не нашел широкого применения в вакуумной газовой динамике из-за высоких требований к ресурсам компьютеров и значительных затрат машинного времени.
Метод статистических испытаний (пробных частиц) широко применяется в молекулярном режиме и алгоритм проведения вычислительных экспериментов хорошо известен. В данном докладе представляется более подробно процедура и алгоритм проведения вычислительных экспериментов как в молекулярном так и в молекулярно-вязкостном режиме по модели [5], которая является развитием статистических и вероятностных подходов к имитационному моделированию течения разреженного газа.
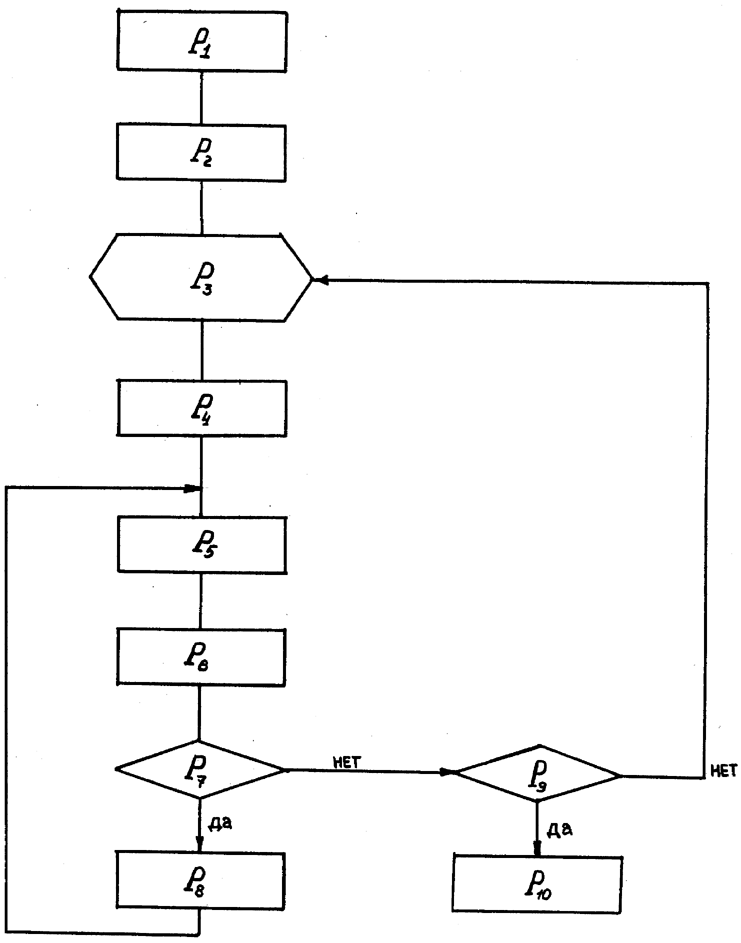
Для проведения вычислительных экспериментов в молекулярном и молекулярно-вязкостном режиме создан комплекс программ в соответствии со следующим алгоритмом, который может быть представлен (рис.1) [5]:
P1 - ввод исходных данных: давления во входном м выходном сeчении элемента и формирование исходных уравнений конфигурации внутренней поверхности элемента; P2 - преобразование уравнений, задающих конфигурацию внутренней поверхности элемента из локальной системы координат в глобальную; P3 - организация цикла по числу испытаний; P4 - определение координат молекулы на плоскости входного сечения и направления траектории движения молекулы при входе в элемента; P5 - определение длины свободного пути молекулы; P6 - определение местоположения молекулы при межмолекулярном соударении или соударении с внутренней поверхностью элемента; P7 - проверка условия выхода молекулы из элемента; P8 -вычисление нового направления траектории движения молекулы; P9 - проверка окончания цикла по числу испытаний; P10 - вывод результатов: вероятности прохождения, проводимости элемента, погрешности вычислительного эксперимента.

В соответствии с данным алгоритмом течение разреженного газа моделируется следующим образом. При средней длине свободного пути молекул значительно больше характерного размера вакуумного элемента при значениях Kn > 100 по данному алгоритму реализуется имитационная модель молекулярного течения. Соударения пробной молекулы наблюдаются только со стенками вакуумного элемента и без межмолекулярных соударений. При δ = 0,01, где δ = 1/Kn, кроме соударений со стенкой, дополнительно наблюдаются первые межмолекулярные соударения. При значениях 0,01 < δ < 0,5 межмолекулярные соударения, как правило, парные, поскольку направление траектории движения молекулы после межмолекулярного столкновения остается равновероятно в полном телесном угле 4π стерадиан. Это свидетельствует о том, что коллективный эффект взаимодействия ансамбля окружающих молекул (Ф) не оказывает влияние на движения отдельных молекул. Таким образом, при значениях 0,01 < δ <0,5 направления движения отдельных молекул изменяются “внутри” потока только в результате парных соударений молекул. По существу эта область является областью применимости модели Г.Берда.
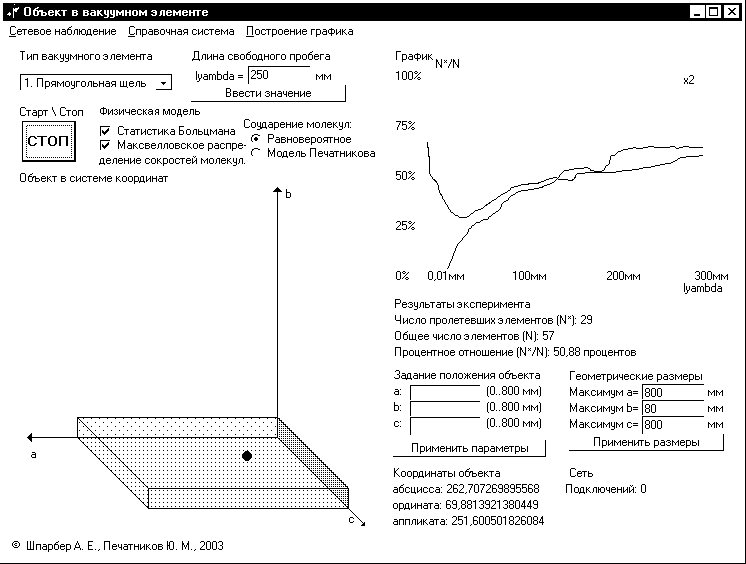
Рис.2
При δ >0,5 на направление движения молекулы после соударения дополнительно оказывает влияние силовое поле межмолекулярного взаимодействия группы окружающих молекул, однако при значениях 0,5 <δ < 10 данное влияние невелико до 10% и модель Г. Берда может быть применена с допустимой, для инженерных расчетов, степенью точности. При δ = 100 более низких числах Кнудсена большинство соударений не являются только парными и коллективный эффект взаимодействия молекул должен быть принят во внимание при моделировании. При направление движения молекул ориентировано по потоку течения разреженного газа.
В настоящее время данный алгоритм и процедура реализованы методами визуального программирования и обладает дружественным интерфейсом (рис.2).
Заключение: Результаты экспериментов показали, что машинное время, затрачиваемое на имитационное моделирование по данному алгоритму, экономится более чем в 100 раз по сравнению с методом прямого моделирования (Г. Берда).
Результаты, получаемые методом вероятностных направлений более точны по сравнению с методом прямого моделирования (Г. Берда).
ЛИТЕРАТУРА
1. Розанов Л.Н., Никитков Н.В., Дзельтен Г.П., Печатников Ю.М. Автоматизация проектирования в машиностроении // Научно-технические вeдомости СПбГТУ, 1996. N3, С.38-41.
2. Печатников Ю.М. Современные методы расчета характеристик вакуумных агрегатов для среднeго вакуума (Обзор) // Вакуумная техника и технология. 2002. т.12, №4, С. 227-234.
3. Печатников Ю.М., Синицын А.А., Тумаров Р.Р. К вопросу внедрения САПР в машиностроение. // Вестник машиностроения. 2002. 9, с.64-66
4. Печатников Ю.М. Концепция проектирования структуры вакуумных систем // Вакуумная техника и технология. 2001. 4, С.3-10.
5. Печатников Ю.М. Вычислительно-эвристический подход к расчету и проектированию вакуумных систем // Научно-технические ведомости С.ПбГТУ.-2002, N1, с.80-87
Предыдущая.......... На главную страницу.............Следующая