Глава 3. Начальный этап применения вакуумной техники в промышленности (1880 - 1915)

Расширившаяся потребность в средствах создания разреженной газовой среды для исследований явилась важным стимулом для совершенствования техники высокого вакуума. Работы выдающихся физиков-экспериментаторов Дж.Дж.Томсона, П.Н.Лебедева и др. продемонстрировали возможность существенного продвижения вперед на пути получения все более низких давлений. Тем не менее, не эти опыты сыграли основную роль в прогрессе вакуумной техники. В последней четверти XIX в научно-технические проблемы, связанные с совершенствованием средств получения вакуума, начинают привлекать внимание значительно более широкого круга учёных, инженеров и изобретателей. В своих воспоминаниях Д.Д.Томсон написал этом процессе следующее: "... потребность в высоком вакууме для электрических ламп привела к тому, что получение высокого вакуума стало делом коммерческой выгоды, а в результате физик имеет в своем распоряжении <...> насосы большой мощности" [87].

Вакуумирование выпускаемых изделий - электрических ламп накаливания - становится промышленным технологическим процессом. Работа над повышением эффективности этого процесса привела к усовершенствованию ртутного и механического поршневых насосов, изобретению геттеров - средств поддержания вакуума в отпаянных лампах. К началу ХХ столетия значительно расширились знания в области сорбции газов и паров твердыми веществами. Была определена сорбционная емкость разнообразных веществ, изучены механизмы физической и химической сорбции, зависимость абсорбции и адсорбции от температуры и т. п. Развитие термодинамики привело к более глубокому пониманию таких важных для вакуумной техники вопросов как диссоциация соединений и восстановление окислов, теплоты образования и испарения и т.п.

В этот период существенно изменились представления о строении материи и среды для распространения излучений и электромагнитных взаимодействий - эфира. Одновременно с "атомизацией" эфира быстрое развитие получила молекулярно-кинетическая теория газов. Уже во второй половине Х1Х в. были сформулированы законы идеального газа, предложена теория реальных газов, разработаны методы расчета количественных характеристик газовых молекул.

1. Вакуумная техника в производстве электрических ламп накаливания

На протяжении ХIХ века изобретателями в разных странах предпринимались попытки использовать для освещения накаливание электрическим током различных проводников. В качестве накаливаемых элементов использовались платиновая и платино-иридиевая проволока, угольные нити, графитовые стержни и другие материалы. Авторы уже первых конструкций ламп накаливания - Деларю (1809), Жобар (1838), де Молейнс (1841) и др. пришли к выводу о целесообразности создания вакуума внутри лампы [88]. Однако откачка с помощью механического поршневого насоса не давала разрежения в колбе, которое могло обеспечить приемлемый срок службы лампы.

В 1854 г. немецкий изобретатель Гебель осуществил вакуумирование лампы с угольной нитью ртутно-поршневым методом. Лампа Гебеля представляла собой длинную стеклянную трубку с впаянными электродами. Трубка заполнялась ртутью, после чего переворачивалась запаянным концом вверх, а нижним - опускалась в сосуд с ртутью. В полости, где находились электроды с нитью накаливания, образовывалась торичеллиева пустота. Эта часть трубки отпаивалась, получалась вакуумная лампа с угольной нитью.

Гебель не был предпринимателем: он не позаботился о получении патента и организации производства своей лампы. По разным причинам сколько-нибудь значительного применения не получили разработки и других изобретателей (в книге Л.Д. Белькинда приводится перечень более двух десятков основных типов ламп накаливания, патенты на которые были выданы в период с 1809 по 1878 г. [89]). Успешно решить комплекс вопросов по изготовлению практически пригодной лампы накаливания и организации системы электрического освещения удалось Т. А. Эдисону. Средством получения вакуума на первой фабрике по производству электрических ламп накаливания, открытой в Менло-парке в 1880 г., служили насосы Шпренгеля [90]. Выбор Эдисоном этого типа насоса объяснялся не только их сравнительно высоким предельным вакуумом, но и возможностью продолжительной работы без оператора. Время откачки лампы было довольно большим: в 1881 г. оно составляло примерно 5 час, в 1896 г. - около 30 мин. Длинные ряды трубок Шпренгеля, каждая из которых вела откачку одной лампы, являлись характерной принадлежностью первых предприятий по выпуску ламп накаливания (рис. 25).

После Всемирной выставки 1881 г. в Париже новая система освещения получает быстрое развитие в Европе. Предприятия, выпускающие лампы накаливания, появляются во Франции, Германии, Англии, Австро-Венгрии, Италии и Голландии. Совершенствование производства осветительной аппаратуры становится "делом коммерческой выгоды". Сотни инженеров и ученых работают над технологическими процессами изготовления лампы накаливания.

В 1894 г. А. Малиньяни получил патент на способ улучшения вакуума в отпаянных лампах [91]. На внутреннюю поверхность ламповой колбы наносилась суспензия красного фосфора в вязкой жидкости. После отключения вакуумного насоса нить лампы прокаливалась при напряжении, превышающем нормальное, давление внутри колбы существенно снижалось в результате поглощения остаточных газов фосфором.

Изобретение Малиньяни существенно изменило процесс изготовления ламп накаливания. Время откачки значительно сократилось, срок службы ламп вырос. В последующие годы было предложено множество других геттеров - веществ, поглощающих остаточные газы в лампах и приборах.

В 1905 г. значительному усовершенствованию подвергся ртутно-поршневой насос. Молодой немецкий физик Вольфганг Геде, впоследствии ставший классиком вакуумной техники, изобрел способ заменить многократное поднимание и опускание сосуда с ртутью вращательным движением [92].

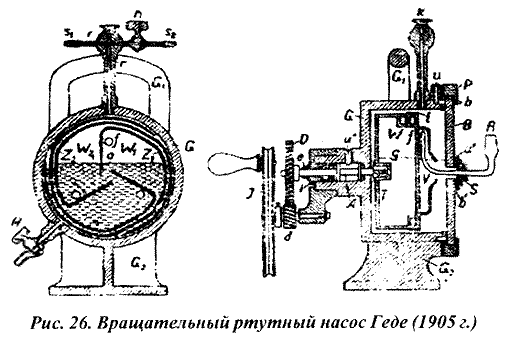
Основной частью вращательного ртутного насоса Геде (рис. 26) является фарфоровый барабан Т, частично заполненный ртутью и приводимый в движение с помощью рукоятки J. При вращении барабана Т (против часовой стрелки) происходит увеличение объема W1, заключенного между поверхностью ртути g и стенкой барабана z1. Воздух из откачиваемого сосуда засасывается в этот объем через отверстие f и трубку R. При дальнейшем движении отверстие f перекрывается ртутью, и воздух выталкивается ртутью через спиральный канал барабана в область форвакуума.

Имея такой же предельный вакуум как насосы Гейсслера и Шпренгеля (~10^-5 мм рт. ст.), вращательный ртутный насос Геде значительно превосходил их по скорости откачки - примерно в 20 раз сравнительно с наиболее распространенной конструкцией Шпренгеля-Кальбаума. В первой четверти ХХ в. ртутный насос Геде широко применялся в исследовательских лабораториях, а также в промышленности для откачки ламп накаливания и рентгеновских трубок. В качестве форвакуумной ступени для насоса Геде первоначально использовался механический поршневой насос Флейсса. К 1908 г. тот же Геде разработал и передал в производство пластинчато-роторный насос с масляным уплотнением, ставший на многие годы основным средством получения предварительного вакуума.

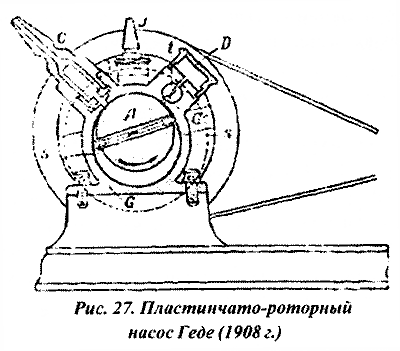
Принцип действия пластинчато-роторного насоса показан на рис. 27. Внутри корпуса насоса G вращается эксцентрично расположенный ротор А. В пазах ротора находятся лопатки S, поджимаемые к поверхности корпуса пружинами. При перемещении лопатки S происходит увеличение объема между ротором и корпусом в левой части насоса, воздух засасывается через входной патрубок С. При дальнейшем движении лопатки S воздух сжимается в правой части насоса и выталкивается через клапан t и патрубок D в атмосферу. Внутри насоса имелось некоторое количество масла, обеспечивающего уплотнение лопаток и частично отвод тепла.

Наибольшее распространение получила двухступенная конструкция пластинчато-роторного насоса, в которой первая ступень имела на выходе атмосферу, а вторая - форвакуум порядка 10-20 мм рт. ст. В этом случае насос Геде обеспечивал предельное остаточное давление порядка 10^-2-10^-3 мм рт.ст.с быстротой откачки порядка 0,15 л/с.

2. Молекулярно-кинетическая теория газов и область низких давлений

Основные представления, положенные в основу кинетической теории газов, были сформированы во второй половине XIX в. В 1856 г. А. Крёнигом была опубликована работа "Очерки теории газов", в которой давалась модель идеальных газов, основанная на представлении о молекулах как упругих шарах [93]. При соударении со стенкой молекула массы m, имеющая среднюю скорость V сообщает стенке импульс mV. Если о стенку ударяются n молекул, то полный импульс, действующий на стенку, будет равен nm?. Это дало основание Крёнигу говорить о давлении газа как импульсе молекул, передаваемом поверхности стенки в единицу времени:

Р=nmV (1)

Спустя год, и тоже в журнале "Annalen der Physik", появилась статья Р. Клаузиуса "О роде движения, который мы называем теплотой" [94]. В этой статье идеи кинетической теории газов получили дальнейшее развитие. Независимо от того, какими являются траектории и скорости отдельных атомов и молекул, теория строится на рассмотрении статистических средних величин. Статистический подход приемлем для анализа энергии молекул, давления на стенку и других характеристик газа.

"Действие каждого отдельного удара вследствие малой массы молекул очень незначительно, но зато число ударов, приходящихся в течение единицы времени даже на самый малый элемент поверхности, доступный нашему наблюдению, очень велико. Отсюда для нашего восприятия создаётся ложное впечатление, будто стенка получает сообщённое ей количество движения не благодаря отдельным толчкам, а под влиянием постоянно действующей силы, направленной изнутри наружу. Эта сила и есть та самая, которую мы называем давлением". Принимая, что молекулы движутся в шести направлениях, перпендикулярных к граням куба, а изменение импульса каждой молекулы при упругом соударении со стенкой равно 2mV, Клаузиус получил следующее выражение для давления газа:

Р=1/3 mnV (2)

Из молекулярно-кинетической теории логично выводились известные газовые законы. При неизменной средней скорости молекул давление должно быть пропорциональным плотности, что подтверждалось законом Бойля-Мариотта. С ростом скорости увеличивается число ударов, а также их энергия. Поэтому давление должно быть пропорционально квадрату скорости.

"Если допустить, что абсолютная температура представляет собой меру живой силы поступательного движения молекул и, следовательно, что она пропорциональна квадрату скорости, то изложенный выше вывод приводит нас к закону Гей-Люссака". Вышеприведённое уравнение для давления, соответственно, может быть записано в следующем виде:

Р = 1/3(nmV²) (3)

Cогласно Клаузиусу, кинетическая модель идеального газа имеет следующие физические характеристики:

"Пространство, действительно заполненное молекулами газа, должно быть исчезающе мало по сравнению со всем пространством, занимаемым газом".
"Время одного столкновения <...>должно быть исчезающе мало по сравнению со временем, протекающим между двумя ударами".
"Влияние молекулярных сил должно быть исчезающе мало".

Весьма условное допущение Клаузиуса о том, что все молекулы движутся с единой средней скоростью, было устранено в 1860 г. Максвеллом. Принимая модель существования "неопределённого количества малых, твёрдых и абсолютно упругих шаров, действующих друг на друга только во время столкновения", Максвелл приходит к выводу, что после большого числа столкновений скорости шаров должны распределяться по закону, схожему с законом Гаусса для распределения случайных ошибок измерения. При различных условиях (меняющихся в первую очередь с температурой газа) существует наиболее вероятная скорость молекул, все остальные скорости группируются в соответствии с законом распределения. В той же работе "Пояснения к динамической теории газов" Максвеллом были даны, кроме того, выражения для определения средней длины пробега молекул, коэффициента внутреннего трения газов [95].

Существенным вкладом в кинетическую теорию газов стала опубликованная в 1873 г. работа Ван-дер-Ваальса "О непрерывности газообразного и жидкого состояния". Проанализировав вероятные отступления от законов идеального газа, он предложил уравнение, содержащее поправки на объём и силы притяжения реальных молекул:

(P+a/V²)(V-b)=RT (4)

В этом уравнении V - молярный объём, слагаемое V² - поправочный член, учитывающий силы притяжения между молекулами, а постоянная b представляет собой меру истинного объёма молекул:

,

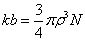где 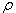- радиус молекулы; N - число молекул в грамм-молекуле (число Авогадро); k cчиталось в конце 19-го века равным .

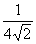Работы Крёнига, Клаузиуса, Максвелла и Ван-дер-Ваальса вместе с выполненными в тот же период исследованиями Грэхэма, Майера, Лошмидта и др., по существу сформировали основные положения и методы кинетической теории газов. Начиная с последней четверти XIX в. кинетическая теория газов развивается "вширь", обращаясь к исследованию многообразных условий течения газов, интерпретации физических процессов в широком диапазоне давлений, температур и т. д. В этот период появились исследования, свидетельствующие, что ряд положений кинетической теории газов требует уточнения для области низких давлений. Работы такого характера, более широко развернувшиеся в ХХ в., стали в определённой степени самостоятельным направлением данной области науки. Мы остановимся лишь на отдельных исследованиях, явившихся существенным вкладом в развитие кинетической теории газов для условий вакуума.

Одним из первых достижений стал анализ явления внутреннего трения или вязкости газа при низких давлениях. В 1875 г. Кундт и Варбург провели эксперимент, свидетельствовавший о том, что затухание колебаний упругой пластинки, вызванное внутренним трением газа, меняет характер в условиях достаточно высокого вакуума. Исследователи предположили, что при очень низких давлениях коэффициент вязкости газа становится функцией давления. Такой вывод вступал в противоречие с одним из основополагающих результатов, полученных к тому времени кинетической теорией газов. При обычных давлениях газа длина свободного пробега L обратно пропорциональна числу молекул, находящихся в единице объёма. Cредняя скорость молекул v зависит только от температуры и молекулярного веса. Расчёты показывали, что для любого газа при постоянной температуре вязкость не зависит от давления и должна увеличиваться с температурой. Это положение, нашедшее экспериментальное подтверждение, стало одним из больших успехов кинетической теории газов. Хорошо известно, что вязкость жидкостей уменьшается с ростом температуры. То, что для газов эта зависимость должна носить обратный характер, стало замечательным выводом теории. Однако этот вывод относился к внутреннему трению в газах при обычных давлениях. Наблюдения Кундта и Варбурга были связаны с созданием высокого вакуума в объёме. Согласно их модели, в таких условиях происходит как бы скольжение газа вдоль пластинки. Тангенциальная сила В, действующая на пластинку в результате внутреннего трения в газе, должна определяться следующим соотношением:

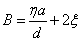, (5)

Где 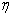- коэффициент вязкости газа, 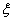- величина, получившая название коэффициент скольжения.

Принципы кинетической теории газов позволяют связать коэффициент скольжения с длиной свободного пробега L:

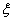=2×0,499(2-f/f)L. (5)

В этом выражении f - коэффициент, максимальное значение которого равно единице.

В случае высокого вакуума, когда L>>d, уравнение примет вид:

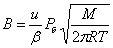, (6)

Таким образом, при очень низких давлениях скорость переноса количества движения от движущейся поверхности к неподвижной прямо пропорциональна давлению и скорости движущейся поверхности. Этот вывод был использован в 1913 г. И. Ленгмюром при создании молекулярного вакуумметра для измерения весьма низких давлений [96].

Близкий по теоретической направленности комплекс исследований был выполнен для изучения теплопроводности газов при низких давлениях. Фундаментальный вывод кинетической теории газов о том, что вязкость газа не зависит от давления, позволил найти простые соотношения между вязкостью, теплопроводностью и диффузией. С точки зрения теории, перенос молекулами от одного слоя к другому какого-то количества движения или кинетической энергии аналогичен и приводит к идентичным уравнениям. Так же как и вязкость, теплопроводность газов в обычных условиях теоретически не должна зависеть от давления.

Практическое постоянство теплопроводности в широком интервале давлений иллюстрируется кривыми, представленными на графике (рис. 28). Кривые показывают потерю энергии в ваттах платиновой проволокой при постоянной температуре (990 °С) в зависимости от давления [97]. В интервале давлений от 80 до 10 см рт. ст. изменение потерь тепла лежит в пределах 10%, тогда как с переходом в область ниже 5 см рт. ст. оно достигает 100%.

Работы по теории теплопроводности газов для условий высокого вакуума были опубликованы в начале ХХ в. М. Кнудсеном и М. Смолуховским. Теория Кнудсена основывалась на анализе механизма переноса энергии отдельными молекулами [98]. Когда молекулы газа, первоначально имеющие температуру Т_i, сталкиваютcя с нагретой поверхностью, температура которой T_s, полный обмен энергией может произойти лишь после многих столкновений. Кнудсеном был введён коэффициент аккомодации 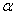, показывающий, насколько полно молекулы успевают приобрести при столкновении среднюю энергию, соответствующую температуре нагретой поверхности. Кнудсен пришёл к следующему выражению для энергии Е₀, переносимой молекулами с 1 кв. см горячей поверхности к холодной поверхности:

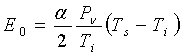, (7)

Где 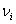- средняя скорость молекул при температуре T_i.

Значения коэффициента аккомодации ? существенно отличаются в зависимости от обработки поверхности металла и рода газа. Для совершенно необработанной (шероховатой) поверхности ? = 1. По опубликованным данным, ? для воздуха и ряда металлов со шлифованной, фрезерованной или травлёной поверхностью составляет от 0,87 до 0,97 [99].

Смолуховский при анализе явления теплопроводности обратился к эффекту "скольжения" газа при умеренно низких давлениях, отмеченному Кундтом и Варбургом. Для передачи тепла между параллельными пластинами, находящимися в разреженном газе, Смолуховский вывел следующее соотношение:

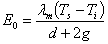, (8)

Где d - расстояние между пластинами; 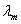- средняя теплопроводность в интервале температур от T_i до T₀.

Коэффициент g определяется выражением:

,

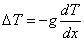где 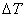- температурный скачок на одной из поверхностей, dT/dx - градиент температуры по нормали к поверхности.

В условиях высокого вакуума:

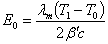. (9)

То есть, при очень низких давлениях величина E₀ не зависит от d и изменяется линейно с давлением Р. К аналогичному результату для области высокого вакуума приводит и расчёт по методу свободных молекул Кнудсена [100]. В рассматриваемый период Кнудсеном, Смолуховским, Геде и другими учёными проводились исследования течения газа через трубы и отверстия при низких давлениях. Кнудсен ввёл понятие "молекулярного потока", имеющего место при таких давлениях, когда длина свободного пробега молекулы по порядку величины равна или больше диаметра трубки или отверстия [101]. В таких условиях, характеризующих также понятие высокого вакуума, течение газа определяется уже не столкновениями молекул между собой, а их взаимодействием со стенками трубки.

Благодаря проведению большого количества теоретических и экспериментальных исследований, во втором десятилетии ХХ в. наметилось появление нового направления данной области науки, связанного с практическим применением принципов кинетической теории газов.